Lecture 1: First-Order Theorem Proving, TPTP, and Vampire

Laura Kovács

First-Order Theorem Proving

We will use the VAMPIRE theorem prover throughout the lecture.

• You can run Vampire natively in the browser here: https://vprover.github.io/vampireGuide/docs/playground
• You can also run Vampire online on SystemOnTPTP here: https://tptp.org/cgi-bin/SystemOnTPTP
• You can download original Vampire here: https://vprover.github.io/download.html

First-Order Theorem Proving. An Example

• Group theory theorem: If a group satisfies the identity $x^2 = 1$, then it is commutative.
• More formally: in a group “assuming that $x^2=1$ for all $x$, prove that $x\cdot y=y\cdot x$ holds for all $x, y$.”
• What is implicit: axioms of the group theory.
  • $\forall x(1\cdot x = x)$
  • $\forall x(x^{-1}\cdot x = 1)$
  • $\forall x\forall y\forall z((x\cdot y)\cdot z = x\cdot(y\cdot z))$

Formulation in First-Order Logic

• Axioms (of group theory)
  • $\forall x(1\cdot x = x)$
  • $\forall x(x^{-1}\cdot x = 1)$
  • $\forall x\forall y\forall z((x\cdot y)\cdot z = x\cdot(y\cdot z))$
• Assumptions:
  • $\forall x (x\cdot x = 1)$

---

• Conjecture:
  • $\forall x\forall y(x\cdot y = y\cdot x)$

In the TPTP Syntax

• The TPTP library (Thousands of Problems for Theorem Provers), http://www.tptp.org contains a large collection of first-order problems.
• For representing these problems it uses the TPTP syntax, which is understood by all modern theorem provers, including Vampire.
• In the TPTP syntax this group theory problem can be written down as follows:

%---- 1 * x = x
fof(left identity,axiom,
! [X] : mult(e,X) = X).
%---- i(x) * x = 1
fof(left inverse,axiom,
! [X] : mult(inverse(X),X) = e).
%---- (x * y) * z = x * (y * z)
fof(associativity,axiom,
! [X,Y,Z] : mult(mult(X,Y),Z) = mult(X,mult(Y,Z))).
%---- x * x = 1
fof(group of order 2,hypothesis,
! [X] : mult(X,X) = e).
%---- prove x * y = y * x
fof(commutativity,conjecture,
! [X] : mult(X,Y) = mult(Y,X)).

First-Order Logic and TPTP

• Language: variables, function and predicate (relation) symbols. A constant symbol is a special case of a function symbol.
  • In TPTP: Variable names start with upper-case letters.
• Terms: variables, constants, and expressions $f(t_1, \ldots , t_n)$, where $f$ is a function symbol of arity $n$ and $t_1,\ldots,t_n$ are terms.
• Atomic formula: expression $p(t_1, \ldots, t_n)$, where $p$ is a predicate symbol of arity $n$ and $t_1, \ldots, t_n$ are terms.
• All symbols are uninterpreted, apart from equality ($=$).

FOL	TPTP
$\bot,\top$	$false, $true
$\neg a$	~a
$a_1 \land \ldots \land a_n$	a1 & ... & an
$a_1 \lor \ldots \lor a_n$	a1 | ... | an
$a_1 \rightarrow a_2$	a1 => a2
$(\forall x_1)\ldots(\forall x_n) a$	! [X1,...,Xn] : a
$(\exists x_1)\ldots(\exists x_n) a$	? [X1,...,Xn] : a

Running Vampire on a TPTP file

is easy: simply use vampire <filename> One can also run Vampire with various options, some of them will be explained later. For example, save the group theory problem in a file group.tptp and try vampire --thanks ADuct25 group.tptp

Proof by Vampire (Slightly Modified)

Refutation found.
251. $false                                                                 [trivial inequality removal 250]
250. mult(sk0,sk1) != mult (sk0,sk1)                                        [superposition 14,159]
159. mult(X0,X1) = mult(X1,X0)                                              [superposition 23,87]
87. mult(X1,mult(X0,X1)) = X0                                               [forward demodulation 79,25]
79. mult(X1,mult(X0,X1)) = mult(X0,e)                                       [superposition 23,20]
25. mult(X0,e) = X0                                                         [superposition 23,13]
23. mult(X0,mult(X0,X1)) = X1                                               [forward demodulation 15,10]
20. e = mult(X0,mult(X1,mult(X0,X1)))                                       [superposition 13,12]
15. mult(X0,mult(X0,X1))=mult(e,X1)                                         [superposition 12,13]
14. mult(sK0,sK1) != mult(sK1,sK0)                                          [cnf transformation 9]
13. e = mult(X0,X0)                                                         [cnf transformation 4]
12. mult(X0,mult(X1,X2)) = mult(mult(X0,X1),X2)                             [cnf transformation 3]
10. mult(e,X0) = X0                                                         [cnf transformation 1]
9. mult(sK0,sK1) != mult(sK1,sK0)                                           [skolemisation 7,8]
8. ?[X0,X1]: mult(X0,X1) != mult(X1,X0) <=> mult(sK0,sK1) != mult(sK1,sK0)  [choice axiom]
7. ?[X0,X1]: mult(X0,X1) != mult(X1,X0)                                     [ennf transformation 6]
6. ˜![X0,X1]: mult(X0,X1) = mult(X1,X0)                                     [negated conjecture 5]
5. ![X0,X1]: mult(X0,X1) = mult(X1,X0)                                      [input(conjecture)]
4. ![X0]: e = mult(X0,X0)                                                   [input(assumption)]
3. ![X0,X1,X2]: mult(X0,mult(X1,X2)) = mult(mult(X0,X1),X2)                 [input(axiom)]
1. ![X0]: mult(e,X0) = X0                                                   [input(axiom)]

• Each inference derives a formula from zero or more other formulas;
• Input, preprocessing, new symbols introduction, superposition calculus;
• Proof by refutation, generating and simplifying inferences, unused formulas $\ldots$

Vampire

• Completely automatic: once you started a proof attempt, it can only be interrupted by terminating the process.
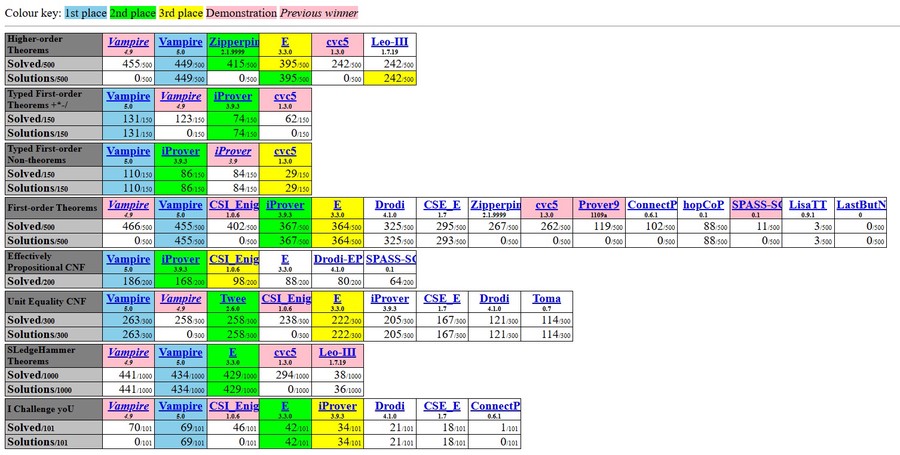
• Champion of the CASC world-cup in first-order theorem proving: won CASC >70 times.

Vampire - The Team at CASC 2025

Vampire - The Team at CAV 2025