Lecture 2: Inference Systems and Selection Functions

Laura Kovács

Inference Systems

• Inference has the form $\displaystyle\frac{F_1 \; \ldots \; F_n}{G}$, where $n\geq 0$ and $F_1, \ldots, F_n, G$ are formulas.
• The formula $G$ is called the conclusion of the inference;
• The formulas $F_1, \ldots, F_n$ are called its premises.
• An inference rule $R$ is a set of inferences.
• Every inference $I \in R$ is called an instance of $R$.
• An Inference system $\mathbb{I}$ is a set of inference rules.
• Axiom: inference rule with no premises.

Inference System: Example

• Represent the natural number $n$ by the string $\underbrace{|\ldots|}_{n\; \text{times}}\varepsilon$

• The following inference system contains 6 inference rules for deriving equalities between expressions containing natural numbers, addition ($+$) and multiplication ($\cdot$).

• $\displaystyle\frac{}{\varepsilon=\varepsilon}$ $(\varepsilon)$

• $\displaystyle\frac{x=y}{|x=|y}$ $(|)$

• $\displaystyle\frac{}{\varepsilon+x=x}$ $(+_1)$

• $\displaystyle\frac{x+y=z}{|x+y=|z}$ $(+_2)$

• $\displaystyle\frac{}{\varepsilon \cdot x = \varepsilon}$ $(\cdot_1)$

• $\displaystyle\frac{x\cdot y = u \;\;\;\;\; y+u=z}{|x\cdot y = z}$ $(\cdot_2)$

Derivation, Proof

• Derivation in an inference system $\mathbb{I}$: a tree built from inferences in $\mathbb{I}$.
• If the root of this derivation is $E$, then we say it is a derivation of $E$.
• Proof of $E$: a finite derivation whose leaves are axioms.
• Derivation of $E$ from $E_1 , \ldots , E_m$ : a finite derivation of $E$ whose every leaf is either an axiom or one of the expressions $E_1 , \ldots , E_m$.

Examples

For example,

$\displaystyle\frac{||\varepsilon + |\varepsilon = |||\varepsilon}{|||\varepsilon + |\varepsilon = ||||\varepsilon}$ $(+_2)$

is an inference that is an instance (special case) of the inference rule:

$\displaystyle\frac{x+y=z}{|x+y=|z}$ $(+_2)$.

It has one premise, $||\varepsilon + |\varepsilon = |||\varepsilon$, and the conclusion $|||\varepsilon + |\varepsilon = ||||\varepsilon$.

The axiom

$\displaystyle\frac{}{\varepsilon + |||\varepsilon = |||\varepsilon}$ $(+_1)$

is an instance of the rule

$\displaystyle\frac{}{\varepsilon + x = x}$ $(+_1)$

Proof, Derivation in this Inference System

Arbitrary First-Order Formulas

• A first-order signature (vocabulary): function symbols (including constants), predicate symbols. Equality is part of the language.
• A set of variables.
• Terms are built using variables and function symbols. For example, $f(x) + g(x)$.
• Atoms, or atomic formulas are obtained by applying a predicate symbol to a sequence of terms. For example, $p(a, x)$ or $f(x) + g(x) \geq 2$.
• Formulas: built from atoms using logical connectives $\neg, \land, \lor , \to, \leftrightarrow$ and quantifiers $\forall, \exists$. For example, $(\forall x)x=0 \lor (\exists y) y>x$

Clauses

• Literal: either an atom $A$ or its negation $\neg A$.
• Clause: a disjunction $L_1 \lor \ldots \lor L_n$ of literals, where $n \geq 0$.
• Empty clause, denoted by $\square$: clause with 0 literals, that is, when $n = 0$.
• A formula in Clausal Normal Form (CNF): a conjunction of clauses.
• From now on: A clause is ground if it contains no variables.
• If a clause contains variables, we assume that it implicitly universally quantified. That is, we treat $p(x) \lor q(x)$ as $\forall x(p(x) \lor q(x))$.

Binary Resolution Inference System

The binary resolution inference system, denoted by $\mathbb{BR}$ is an inference system on propositional clauses (or ground clauses).

It consists of two inference rules:

• Binary resolution, denoted by BR:
  • $\displaystyle\frac{p\lor C_1 \;\;\;\; \neg p \lor C_2}{C_1 \lor C_2}$ $(BR)$
• Factoring, denoted by Fact:
  • $\displaystyle\frac{L \lor L \lor C}{L \lor C}$ $(Fact)$

Soundness

• An inference is sound if the conclusion of this inference is a logical consequence of its premises.
• An inference system is sound if every inference rule in this system is sound.
• $\mathbb{BR}$ is sound.
• Consequence of soundness:
  • let $S$ be a set of clauses.
  • If $\square$ can be derived from $S$ in $\mathbb{BR}$, then $S$ is unsatisfiable.

Example

Consider the following set $S$ of clauses:

• $\{\neg p \lor \neg q,\;\; \neg p \lor q,\;\; p \lor \neg q,\;\; p \lor q\}$

Is S unsatisfiable?

The following derivation derives the empty clause from this set:

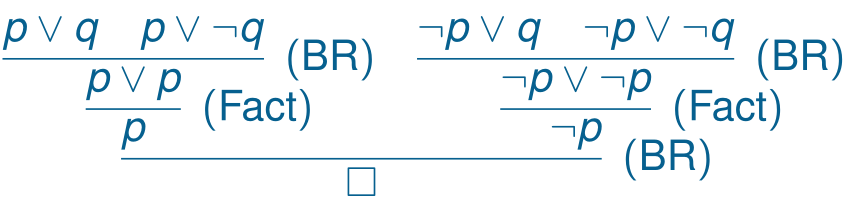
Hence, this set $S$ of clauses is unsatisfiable.

Exercise

Consider the following set $S$ of clauses:

• $\{\neg p \lor \neg q,\;\; \neg p \lor q,\;\; p \lor \neg q,\;\; p \lor q\}$

Show that there exists an infinite number of different $\mathbb{BR}$ derivations of the empty clause $\square$ from the clauses of $S$.

Can this be used for checking (un)satisfiability?

1. What happens when the empty clause cannot be derived from $S$?
2. How can one search for possible derivations of the empty clause?

---

1. Completeness.
   • Let $S$ be an unsatisfiable set of clauses.
     • Then there exists a derivation of $\square$ from $S$ in $\mathbb{BR}$.
2. We have to formalize search for derivations.

However, before doing this we will introduce a slightly more refined inference system.

Selection Functions

A literal selection function is a function that selects literals in a clause.

• If $C$ is non-empty, then at least one literal is selected in $C$.

We denote selected literals by underlining them, e.g.,

$$\underline{p} \lor \neg q$$

• Note: selection function does not have to be a function.
  • It can be any oracle that selects literals.

Binary Resolution with Selection

We introduce a family of inference systems, parameterised by a literal selection function $\sigma$.

The binary resolution inference system, denoted by $\mathbb{BR}\sigma$, consists of two inference rules:

• Binary resolution, denoted by $BR$
  • $\displaystyle\frac{\underline{p}\lor C_1 \;\;\;\; \underline{\neg p} \lor C_2}{C_1 \lor C_2}$ $(BR)$
• Positive factoring, denoted by $Fact$:
  • $\displaystyle\frac{\underline{p} \lor \underline{p} \lor C}{p \lor C}$ $(Fact)$

Completeness?

Binary resolution with selection may be incomplete, even when factoring is unrestricted (also applied to negative literals).

Consider this set of clauses:

$$\begin{array}{ll} (1) & \neg q \lor \underline{r}\\ (2) & \neg p \lor \underline{q}\\ (3) & \neg r \lor \underline{\neg q}\\ (4) & \neg q \lor \underline{\neg p}\\ (5) & \neg p \lor \underline{\neg r}\\ (6) & \neg r \lor \underline{p}\\ (7) & r \lor q \lor \underline{p}\\ \end{array}$$

It is unsatisfiable:

$$\begin{array}{ll} (8) & q \lor p & (6,7)\\ (9) & q & (2,8)\\ (10) & r & (1,9)\\ (11) & \neg q & (3,10)\\ (12) & \square & (9,11) \end{array}$$

Note the linear representation of derivations (used by Vampire and many other provers).

However, any inference with selection applied to this set of clauses give either a clause in this set, or a clause containing a clause in this set.

Literal Orderings

Take any well-founded ordering $\succ$ on atoms, that is, an ordering such that there is no infinite decreasing chain of atoms:

$$A_0 ≻ A_1 ≻ A_2 \succ \cdots$$

In the sequel $\succ$ will always denote a well-founded ordering.

Extend it to an ordering on literals by:

• If $p \succ q$, then $p \succ \neg q$ and $\neg p \succ q$;
• $\neg p \succ p$.

Example: Given $p_6 \succ p_5 \succ p_4 \succ p_3 \succ p_2 \succ p_1$. What is the extended ordering on literals?

Exercise: prove that the induced ordering on literals is well-founded too.

Orderings and Well-Behaved Selections

Fix an ordering $\succ$. A literal selection function is well-behaved if either

• a negative literal is selected,

$$\text{OR}$$

• all maximal literals (w.r.t $\succ$) must be selected in C.

To be well-behaved, we sometimes must select more than one different literal in a clause. Example: $p \lor p$ or $p(x) \lor p(y)$.

Completeness of Binary Resolution with Selection

Binary resolution with selection is complete for every well-behaved selection function.

Consider our previous example:

$$\begin{array}{ll} (1) & \neg q \lor \underline{r}\\ (2) & \neg p \lor \underline{q}\\ (3) & \neg r \lor \underline{\neg q}\\ (4) & \neg q \lor \underline{\neg p}\\ (5) & \neg p \lor \underline{\neg r}\\ (6) & \neg r \lor \underline{p}\\ (7) & r \lor q \lor \underline{p}\\ \end{array}$$

A well-behave selection function must satisfy:

1. $r \succ q$, because of $(1)$
2. $q \succ p$, because of $(2)$
3. $p \succ r$ , because of $(6)$

There is no ordering that satisfies these conditions.

Example

Let $p, q$ be boolean atoms and let $S$ be the following set of ground formulas:

$$\{\neg p \lor \neg q,\;\; \neg p \lor q,\;\; p \lor \neg q,\;\; p \lor q\}$$

Take any ordering such that p ≻ q and any selection function $\sigma$ over $S$ such that

$$\{\neg p \lor \underline{\neg q},\;\; \underline{\neg p} \lor q,\;\; p \lor \underline{\neg q},\;\; \underline{p} \lor q\}$$

(a) Is $\sigma$ a well-behaved selection function over $S$? $\\$ (b) How many inferences of $\mathbb{BR}σ$ are applicable to $S$?